The two solid state relays that we ordered arrive today. They are of type SSR-25DA 25Amp 380V which are easily driven from Arduino digital output pin. The package also provides some multi-input wires that can be used to connect to our micro-controller.
Also, today we study further on how to implement the temperature profile of the solder paste that we have. Basically, we will use a very simple method that is to apply heat if the temperature is below the set point and turn off heating if the temperature is above the set point. Our oven will need to keep doing this process of reading the temperature, comparing with the corresponding set point from the profile, and then adjust correctly, either higher up or lower down. This method is widely known as the “Bang-Bang Control” and the most common way to achieve it is using the PID controller.
The PID controller stands for “Proportional, Integral and Derivative.” Basically, it calculates an error value as the difference between a measured process variable (which in this case is the oven’s temperature at any point) and a desired set point (the corresponding point from the temperature profile). The controller then attempts to minimize the error by adjusting the process through use of a manipulated variable.
The output of the PID controller is calculated as the sum of the proportional, integral and derivative terms.
Proportional term:
The proportional term produces an output value that is proportional to the current error value. The proportional response can be adjusted by multiplying the error by a constant Kp, called the proportional gain constant.
Integral term:
The integral in a PID controller is the sum of the instantaneous error over time and gives the accumulated offset that should have been corrected previously. The accumulated error is then multiplied by the integral gain (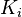
) and added to the controller output.
Derivative term:
The derivative of the process error is calculated by determining the slope of the error over time and multiplying this rate of change by the derivative gain Kd. The magnitude of the contribution of the derivative term to the overall control action is termed the derivative gain, Kd.
Below is the basic block diagram for the tuning loop of a PID controller:
I found the most recent version of the aArtisanQ_PID program that Nick Brenn also used for his coffee roaster project:
