ICP-MS: Lanthanide Interference Corrections

This page is a legacy of when we used to have a single-quad ICP-MS. These interference corrections were very helpful in producing good REE results. Nowadays, with our two-quad + gas reaction cell instrument, we just analyze all the REE in oxygen gas, mass-shift mode. That works beautifully well.

Barium and the lanthanides are relatively strong oxide-formers. That is, ions like Ba⁺ and Ce⁺ react with oxygen in the plasma to form small proportions of BaO⁺ and CeO⁺. The dominant masses of the oxide ions are 16 mass units higher than the isotope of the metal in the oxide. In the figure below, you can see that Ce has 4 naturally occurring isotopes (red bars) at masses 136, 138, 140, and 142. ¹⁴⁰Ce is the most abundant isotope and is the one usually used for quantitative analysis. Pr has only 1 naturally occurring isotope, ¹⁴¹Pr (blue bars). These five M⁺ ions ions combine with ¹⁶O to form from five different mass oxide ions (MO⁺). For example: ¹³⁶Ce⁺ becomes ¹³⁶Ce¹⁶O⁺ at mass 152 (= 136 + 16).

Figure 1. MO⁺/M⁺ ratios from the oxide calibration intensities in Table 1. For the explanation of the importance of the blue value, see text below and Table 4.

Naturally there are also small contributions at other masses from ¹⁷O and ¹⁸O, which are 1 and 2 mass units higher than the ¹⁶O oxides. Hydroxides, such as ¹³⁶Ce¹⁶OH⁺ at mass 153, can also be important. Neither of these are shown here.

CeO⁺ at mass 152 interferes with ¹⁵²Sm analysis, and CeO⁺ at mass 158 interferes with ¹⁵⁸Gd analysis. Oxides shown at masses 154, 156, and 157 are unimportant in this example because they aren’t used for quantitative analysis. There is no interference shown for ¹⁵⁹Tb, although small quantities of ¹⁴¹Pr¹⁸O⁺, ¹⁴²Ce¹⁷O⁺, and ¹⁴²Ce¹⁶OH⁺ do interfere at that mass. Clearly for quantitative analysis of the metals, we need a method of stripping away the interferences from the M⁺ signals.

Figure 2. In this example, a rock with chondritic Ba and lanthanide concentrations is analyzed using pure standards. Uncorrected, the result would be the red line rather than the actual black line.

Figure 3. In this more extreme example, light REE enrichment causes more severe oxide interferences on less abundant heavier REE. This, coupled with much higher Ba concentrations, leads to a substantial divergence of the uncorrected red curve compared to the correct black curve.

Figure 4. In this last example, strong light REE enrichment and very high Ba concentrations results in severe middle REE interferences: on Sm and Eu from BaO, and from lanthanide oxides for Eu and all others. It should be pretty obvious that corrections are vital for producing reasonably smooth chondrite-normalized REE patterns.

The simplest way to determine the size of the interferences at analyzed masses was to measure them directly by analysis of pure, single element solutions. This has the advantage of taking into account the instrument response curve, among other variables. Then, all you have to know is what isotopes you want to analyze, see how big the interferences are at those masses, and calculate how to subtract them from the total signal at each mass of interest.

In Table 1, below, data were obtained by analyzing 15 single element solutions (Ba-Lu), representing the data columns. The rows show signal intensities at each analyzed mass for each of the 15 solutions (signals in cps, corrected for internal standard drift, blanks subtracted). Blank subtraction yields a few negative values. The solution concentrations were 100 ppb for Ba, and 5 ppb for all other elements.

Table 1. Count rate. This is an image, not an actual table.

In Table 1, taking the ratio of the MO⁺ signals in the blue boxes, to the M⁺ signals in the immediately overlying yellow boxes, yields MO⁺/M⁺ ratios, shown in Table 2, below. The work needed to derive all these MO⁺/M⁺ ratios is considerable, and so it’s done rarely. The MO⁺/M⁺ ratios in Table 2 are referred to hereafter as the oxide calibration values. For the importance of the blue value in Table 2, see text below and Table 4.

Table 2, Ratios of count rates. This is an image, not an actual table.

Once we have the values in Table 2, we can calculate the size of the oxide or hydroxide interference as follows:

Equation 1.

Where:

MO⁺_cps,cal = Oxide or hydroxide interference intensity (in cps) determined during oxide interference calibration (e.g., ¹⁴²Ce¹⁶O⁺ at ¹⁵⁸Gd⁺).

M⁺_cps,cal = M⁺ intensity (in cps) during oxide interference calibration at the mass used for quantitative analysis (e.g., ¹⁴⁰Ce), determined during oxide interference calibration. Note that the mass used for quantitative analysis does not have to be the mass producing the interference.

M⁺_cps,analyzed = M⁺ intensity determined during actual quantitative analysis of unknown samples.

The [MO⁺_cps,cal/M⁺_cps,cal] ratios are therefore empirical, dimensionless correction factors that can be used for unknown samples later on (Table 2). The absolute instrument sensitivity can vary while still preserving the proportion of oxides produced.

There is one problem with this method: the MO⁺/M⁺ ratios are not constant; they vary with a wide variety of conditions, including argon gas purity, spray chamber temperature, nebulizer gas flow, the nebulizer efficiency, and so on. Therefore, the correction factors themselves need adjustment each time lanthanides are analyzed. The graph below shows two calibration runs done to determine MO⁺/M⁺. Basically, the graph below is Table 2, determined two different times several months apart. Although the two different runs had MO⁺/M⁺ ratios different by a factor of ~1.5, the changes for all of the interferences was approximately the same: ~1.5. As a result, all of the MO⁺/M⁺ ratios lie close to a straight line. Therefore, if we know the slope of this line on any given day during a run of unknowns, then we can correct the correction factors and accurately determine the sizes of the interferences that day.

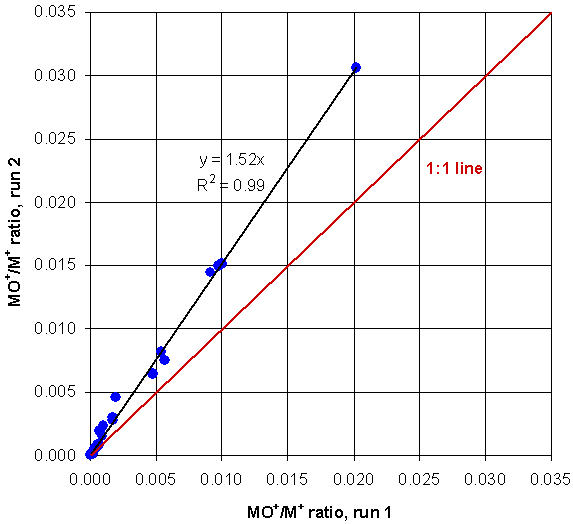
Figure 5. One calibration vs. another calibration done months later. The ratios lie close to a straight, black line at a slope of about 1.5. The difference between the two interference size determinations is simply the line slope.

Determining the correction factors is easily done before a run by first analyzing a pure solution of a lanthanide, such as ¹⁴⁶Nd⁺, and its oxide at ¹⁵⁸Gd⁺. You may notice that 158 is not 16 mass units higher than 146. That is because the oxide at ¹⁵⁸Gd⁺ is from ¹⁴²Nd¹⁶O⁺ (mass 158), not from ¹⁴⁶Nd¹⁶O⁺ (mass 162). It does not matter that our correction factor is derived from ¹⁴⁶Nd⁺ rather than from the Nd isotope actually producing the oxide, because Nd isotope proportions are constant in nature (or nearly so).

What we need to do now is analyze a pure ~5 ppb Nd solution before running our unknowns, and measure the signal for ¹⁴⁶Nd⁺ and ¹⁵⁸Gd⁺ (= ¹⁴²Nd¹⁶O⁺). This new ¹⁴²Nd¹⁶O⁺/¹⁴⁶Nd⁺ ratio will probably be different from the ratio determined during an earlier oxide calibration, such as shown in Table 2.

Equation 2

Where:

C = Correction factor that corrects all of today’s MO⁺/M⁺ proportions to those measured during the oxide calibration done most recently, perhaps months ago, according to the linear relationship shown in Figure 5.

Numerator = Today’s determined NdO⁺/Nd⁺ ratio, determined at masses 158 and 146, respectively.

Denominator = NdO⁺/Nd⁺ ratio, determined originally during the oxide calibration done most recently, perhaps months ago. These values are also measured at masses 158 and 146, respectively.

Now we have the MO⁺/M⁺ proportions for all oxide and hydroxide interferences of Ba, the lanthanides, Hf, and Ta (determined some time ago during the oxide calibration), and we have the correction factor (determined today). During the analysis of unknowns, the signals on the analyzed element masses (yellow in Table 1) are used to calculate the oxide interference on all pertinent higher masses (blue in Table 1) by the equation:

Equation 3.

Variables defined above.

These values can then be subtracted from the signals at the masses having the interferences, to yield the actual signal produced by M⁺ ions, stripped of the oxide interferences:

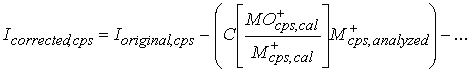
Equation 4.

Where:

I_{corrected,cps} = Intensity of the M⁺ signal at a given mass, in cps, after removal of the interferences.

I_original,cps = Intensity of the total signal at a given mass, in cps, before removal of the interferences.

The ellipsis (…) at the end of Equation 4 indicates additional interference corrections for additional oxide species. For example, Nd and Sm both produce oxides that interfere with ¹⁶³Dy, hence, two correction terms in Equation 4. Referring to Tables 1 and 2:

The interference from Nd on mass 163 is 23/56574 = 0.00041.
The interference from Sm on mass 163 is 196/83404 = 0.00235.
See the Dy row in Table 4.

Correction factor C is determined each day using the pure Nd solution. The actual intensity at mass 163, due exclusively to ¹⁶³Dy is:

¹⁶³Dy = (original mass 163 intensity) – (C * 0.00041 * intensity of ¹⁴²Nd) -(C * 0.00235 * intensity of ¹⁵²Sm). Equation 5.

These concepts are all well and good, but what do you actually need to do before analyzing a bunch of samples?

Item	Example value	Notes
Today’s measured Nd/Gd (A)	0.01875	Measured today on a ~5 ppb Nd solution
Original calibration Nd/Gd (B)	0.02540	The calibration in blue in Table 2, determined some time in the past
Today’s correction factor: A/B = C	0.738	The C value that you type into the interference corrections in the software, shown in Table 4

Table 3. This is what you need before doing a run analyzing REE.

Table 4, below, shows all of the oxide correction equations for Ba, the lanthanides, Hf, and Ta. The equations are more-or-less in the format that they appear in the PerkinElmer Elan 6100 software, correction equations section. C is all you need to change. Presumably, other software has places to enter similar kinds of corrections.